When
many people first see STEM, they are often overwhelmed by the potential of the software
and get caught up in the details of modelling a telecoms network. To help overcome
this, we ran a session at the STEM User Group 2006 that was aimed at new users and
focussed on an area completely different from telecoms: modelling a low-cost airline
business. In this way, we were able to focus on the key business-modelling features
of STEM. Based upon feedback from the session, this novel approach was a tremendous
success in allowing people to see how STEM works, and how it can be applied to telecoms.
A few key principles are behind every STEM model
Almost every business exists to serve a market by providing a service which will
generate revenue. In order to provide this service, a company will incur costs.
These costs can either be direct costs (e.g. costs of goods sold) or may arise from
resources that the company must operate in order to provide the service (e.g. the
cost of a plane for an airline).
The key to understanding any business is to understand three things: the sources
of revenue, the sources of costs, and the relationship between the revenues and
costs. These three concepts are handled in STEM using the following methods (simplified
here for ease of understanding):
|
Sources of revenue
|
In STEM, all revenue is associated with services that the business provides. Each
service has a set of individual inputs, with the key ones being the number of customers
(in the example business, the number of individual customers), their annual demand
(e.g. total flights in a year), the peak demand (e.g. flights in the busiest day),
and a number of tariffs which are split into the categories of connection, rental
and usage.
|
|
Sources of costs
|
Resources are used in STEM to represent all costs, and have a wide range of cost
inputs such as capital expenditure, maintenance costs, lease costs, etc. In addition,
resources are characterised by their capacity (the driver for the costs) and, in
the case of assets, their lifetimes.
|
|
Links between revenue and costs
|
The relationships between revenues and costs are modelled by linking different services
and resources. The outputs which can be used include:
- for services – number of customers, annual demand, peak demand
- for resources – total units installed, new units this year, total capacity installed,
new capacity this year, used capacity and utilisation.
In addition to these primary drivers, a wide range of other constraints can be applied
that will affect the costs.
|
Business model for a low-cost airline: assumptions
|
Short-haul flights with a quick turn-around time
|
To reduce costs, the carrier only operates short-haul flights of less than 3 hours flying time, which allows all its planes
to return to their home airport each night. High utilisation of the aircraft is
achieved by reducing turn-around times between flights to less than 30 minutes.
The model assumes each aircraft can operate 6 flights per day, and can operate for
80% of the time.
|
|
No multi-leg fares
|
The airline does not sell fares that allow a stop-over or any transfer between flights:
this minimises financial risk if a flight is delayed. Therefore, in the model, demand
is measured in single flights.
|
|
Single type of aircraft
|
To reduce operating costs and staff training, the airline only operates a single
type of aircraft. We assume these are similar to a Boeing 737, with a capacity of
200 passengers, a lease cost of EUR5.6 million per annum, and an annual maintenance
charge of EUR450 000.
|
|
Out-of-city airports
|
Flights are made mainly to secondary airports that are some distance away from city
centres: this reduces the fees paid to airport operators. We assume airport fees
amount to EUR1000 per flight.
|
|
Reduced services from onboard staff
|
Staff costs are reduced by offering fewer additional services. The model assumes
8 staff (including pilots) are required for each operational aircraft. Staff can
work 60% of the time and have a fully loaded cost of EUR 80 000 per annum.
|
|
No refreshments included
|
To minimise basic fares, no free refreshments are provided. 30% of passengers purchase
refreshments, at an average price of EUR6, with a gross margin of 70%.
|
|
Other costs
|
Other major costs include fuel costs of EUR2200 per flight, tax of EUR5 per passenger,
and marketing of EUR2 per passenger.
|
|
Low average fares
|
Perhaps the key aspect of a low-cost airline business is the large amount of price
discrimination that is used to encourage high load factors (percentage of seats
sold). This model, however, does not aim to model this in detail, and simply assumes
an average fare of EUR65 per flight. It assumes the number of passengers increases
to 14 million within 5 years, and 56 million within 20 years.
|
|
Number of routes operated
|
The number of routes starts at 5 and increases to over 400. If an airline operates
a large number of routes, it is inevitable that some will be busier than others,
and the model attempts to capture this in-homogeneity of demand. Based upon industry
benchmarks, we assume that the load factor tends towards about 80%.
|
Creating the model
The graphical nature of STEM allows us to show the whole model in a single diagram,
as shown below.
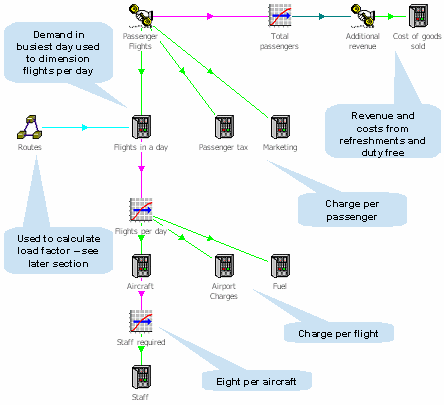
The low-cost airline model: initial design
In order to keep the modelling simple, we assume that prices and tariffs (revenue
per flight) remain constant over time: the only inputs that vary over time are the
number of passengers and the number of routes operated.
Earlier we discussed the different types of drivers can be deployed in a STEM model.
A number of these are used in this model:
- busy period demand is used to dimension the number of flights per day
- annual demand is used to dimension the passenger taxes and marketing costs
- the number of flights per day (i.e. units installed) is used to dimension the number
of aircraft
- the total number of aircraft is used to dimension the staff requirement.
In order to model the number of spare (i.e. unsold) seats per flight, we assume
that for each route there will be one-third of a flight’s worth of unsold seats.
For example, if there are 100 flights on 30 routes, with 200 seats per flight, we
assume there will be 2000 (= 1/3 × 30 × 200 ) spare seats per day. This equates
to a load factor of 90% (= (200 × 100) – 2000 / (200 × 100)).
The assumptions for the number of routes and the number of flights required are
shown below.
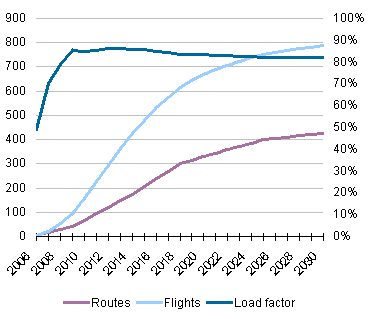
Change in load factor as number of routes and flights increase
The chart shows that the load factor increases rapidly from about 50% to almost
90% and then falls over time. This decline occurs because after the first few years
the expansion has to occur on the less popular routes, resulting in lower load factors.
In reality it may be possible to increase the load factor on the less popular routes,
but this is likely to be at the expense of the average revenue per flight.
Viewing initial results
Using the built-in Results program, it is possible to quickly plot many key results,
such as those shown below.
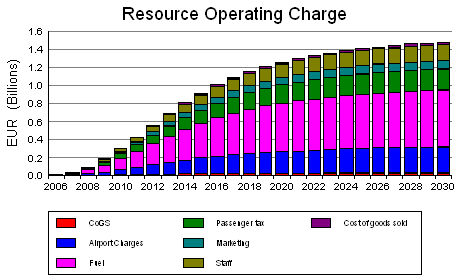
Total costs (opex plus depreciation) for each cost category
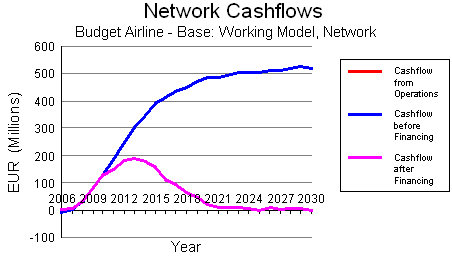
Predicted cash flow
Adapting the model
Within the workshop we made a number of modifications in order to investigate the
business model further. These are discussed briefly below:
|
Additional marketing spend
|
We modified the model to look at the effect of spending more on marketing, to increase
passenger demand. This was done by creating an alternative scenario for the number
of passengers and the marketing spend per passenger. The results showed that the
benefits of increased cash flow in early years outweighed the negative impact of
reduced long-term margins from increased marketing spend.
|
|
Purchasing rather than leasing aircraft
|
The initial model assumed that aircraft are leased. In fact many large, established
airlines purchase their aircraft: this helps to reduce financing costs in the long
term. To examine this option, we built scenarios in which the capital and lease
costs of the aircraft resource were defined to reflect the two purchase methods.
After accounting for the value of the fixed assets (aircraft), which could be sold
at a later date, it was found that purchasing aircraft instead of leasing them is
preferable. However, this is only the case if the cost of capital is relatively
low.
|
|
Customer segmentation
|
STEM can replicate (i.e. copy) part of a model at run-time so that segmented (or
geographical) analysis can be carried out. We used this feature used to model three
different market segments: those that are inelastic to price (e.g., business travellers),
those with a moderate elasticity (e.g. average holiday passengers), and those that
are very price elastic (e.g. short-break travellers). The model was then modified
so that the price for each segment fed back to the demand, in order to investigate
the optimum tariffs for the different segments.
|
Conclusions
Over the course of two short workshops we successfully built a model of a low-cost
airline business in STEM. By concentrating on a topic away from telecoms it was
easier to focus on the structure of the model, and how it deploys resources to satisfy
a service demand. It can be seen that with a little lateral thinking, the basic
building blocks of STEM (services, transformations and resources) can be applied
to almost any business. Other businesses that could be modelled easily in STEM include:
parcel couriers, taxis, hire cars, cinemas and restaurants. We would encourage STEM
users to attempt one of these models to help improve their understanding of STEM.
We would happily publish any interesting models in future editions of this newsletter.